第六期：精读Pentacam之角膜屈光力

第六期：精读Pentacam之角膜屈光力

！复制过来公式完全没有了，原文可以参见PDF文件！

Pentacam中常见的屈光力有：模拟角膜镜读数(SimK)、角膜净屈光力(KTNP)、等效角膜屈光力(EKR) 、总角膜屈光力(TCRP)，如下拉果打开屈光力图的菜单还会发现有前表明轴向曲率、前表明切向曲率等众多屈光力，为何表达角膜的折射能力要用这么多屈光力？其实，这本身就说明角膜的屈光力不易测量且很复杂还多变。

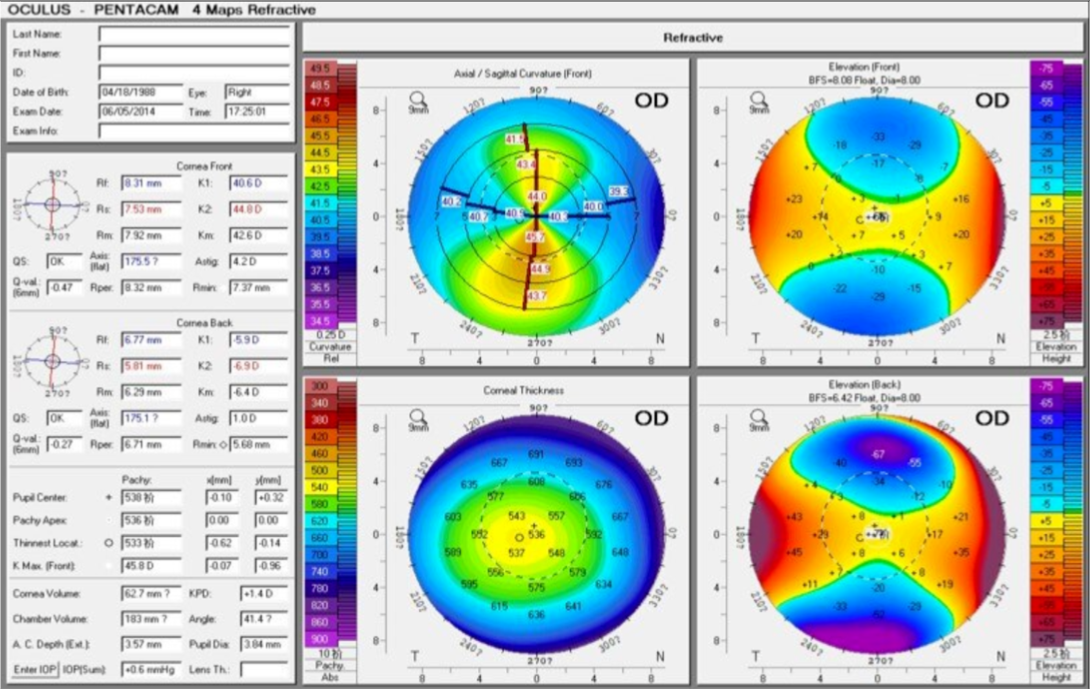
常规四联图中前表面曲率图(左上角轴向曲率图或失状曲率图)，可以读得Rf=8.31mm，K1=40.6D，其计算就是（n2-n1）/r=1000（1.3375-1）/8.31=40.6D，具体的推导过程如下(高斯光学定理)：

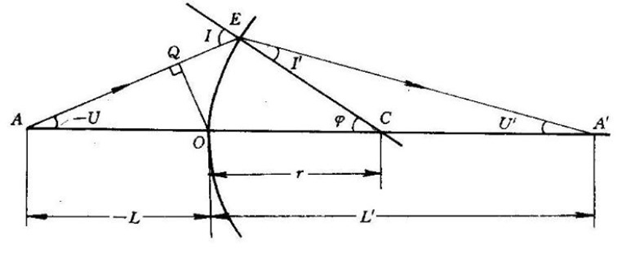
（近轴光线从A点出发经凸球面镜E点折射成像在A’，EC为经过球心C的法线，根据斯涅尔定律(折射定律)知nsinI=n’sinI’(1)

近轴时I≈sinI，则nI=n’I’(2)

I=U+φ，I’=φ-U’，带入(2)式得

n(U+φ)=n’(φ-U’)，近轴时EO⊥AA’，U≈tanU，则

n+n’=(n’-n)，其中，AO为物距l，OA’为像距l’，OC、EC为半径r，物距和像距方向相反，整理可得

+=

假定近轴的物点位于无穷远处，则像点A’即为该凸球面镜的第二焦点，OA’=l’=f’,化简上式即得

=，即为球面的光焦度，这就是单球面成像的高斯公式，即P==，这即是透镜的面屈光力，其实，高斯光学也是光路追迹的一级近似结果。）

该K值即为模拟角膜镜度数，其计算是利用角膜曲率计指数1.3375计算而得，而非真实的角膜曲率1.376。不过，大多非移轴相机地形图的角膜曲率K值都是这个，经典的人工晶体计算公式也是用的该K值，有其历史原因。

相对于轴向曲率，就有切向曲率，切向曲率是用该点的真实曲率半径计算而得，一般较轴向曲率值要高，不过，切向曲率受检查偏位影响较小，较轴向曲率更能反映细微的变化，常用于圆锥角膜等疾病的诊断中，遗憾的是，不能用于晶体度数公式的计算。

由上也可以看出，计算时角膜半径只有一个，并未真实考虑角膜前后表面半径这一具体情况，所以其结果并不准确，他把”测得”的角膜前表面的曲率值认为是整个角膜的曲率，那还有更精确的值吗？

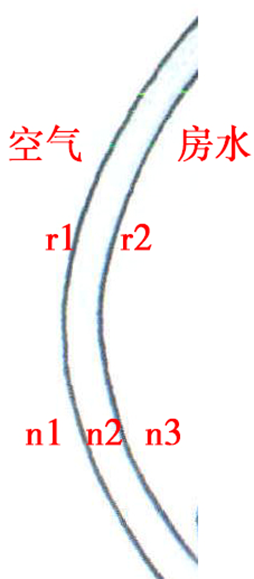
由此产生了角膜净屈光力，计算公式为：(n2-n1)/r1+(n3-n2)/r2，取其角膜真实折射率1.376，可以看出，该屈光力应用了角膜的真实折射率，且考虑了角膜前后表面这一真实因素，其结果理论上要高于模拟角膜镜度数K值，不过净屈光力没有考虑角膜厚度，且没有考虑散光轴向等因素，其结果仍不能代表真实的角膜K值，遗憾的是，该K值也不能用于晶体度数的计算公式进行度数的计算。

如果要考虑角膜的厚度，有什么好的方法来计算角膜的屈光力吗？这里我们把角膜想象成一个厚透镜，厚透镜的等效光焦度为F=F₁+F₂-F₁F₂，其中，前表面光焦度F₁=，后表面光焦度F₂=，这里厚度就是角膜的厚度。

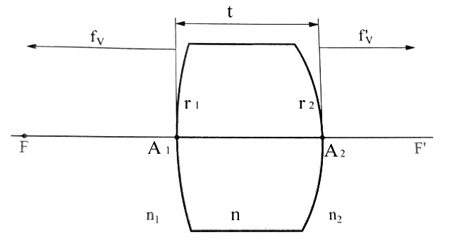
如果不考虑角膜的厚度，即t=0，其屈光力F=F₁+F₂，亦即净屈光力，由此可见，净屈光力要小于考虑角膜厚度的等效光焦度(因为后表面为负值)。由此也可见，净屈光力低估了角膜的真实屈光力，即便如此，该厚透镜仍未考虑角膜不规则的情况，也并不是前后表面屈光力的矢量和，即只考虑了前后表面都是球面的情况，所以也不能反映真实的角膜曲率。

这里插入一个小插曲，在透镜的屈光力中，还有一个屈光力叫“面屈光力”，虽然角膜有前后表面，我们可以把后表面的屈光力“移位”到前表面，或者把前表面的屈光力“移位到”后表面，用移位后的前表面屈光力或者后表面屈光力来代替角膜的屈光力，亦即通常所说的顶点光焦度的换算。

前顶点屈光力FVP=前表面屈光力(F₁)+后表面移动到前表面位置的屈光力(F₂’)，这里以Gullstrand模型眼1加以计算，也可以以地形图中的Km、Rm或其他值进行计算，角膜厚度(顶点厚度)536。

FVP=F₁+=1000+=41.13D，较角膜模拟镜读数42.6D小。

后顶点屈光力BVP=后表面屈光力(F₂)+前表面移动到后表面位置的屈光力(F₁’)：

BVP=F₂+=1000+=42D，较角膜模拟镜读数42.6D接近。

当然，还可以同时移动前后表面到角膜厚度内的任何位置，不过，SimK是角膜镜影像第6、7、8环最大屈光力及其垂直三环曲率的平均值，较顶点屈光力有一定的差距。通过推理和计算可知，角膜的屈光力应该在41.13~42D之间应该是一个较准确的数字，同时也可以看出，SimK值的42.6D应该是高估了角膜的屈光力。

等效角膜屈光力(EKR)是Holladay教授基于Pentacam平台研发的角膜屈光力，为Pentacam所特有，以瞳孔为中心采用光路追迹原理，考虑了角膜前后表面、角膜非球面性以及角膜真实屈光指数，并根据B/F ratio=82.2%进行了优化所得，该值对于用标准模型眼计算的SimK值是等效的，即所谓的EKR，该值可以用于经典的计算公式，包括手术眼(屈光术后)和非手术眼。

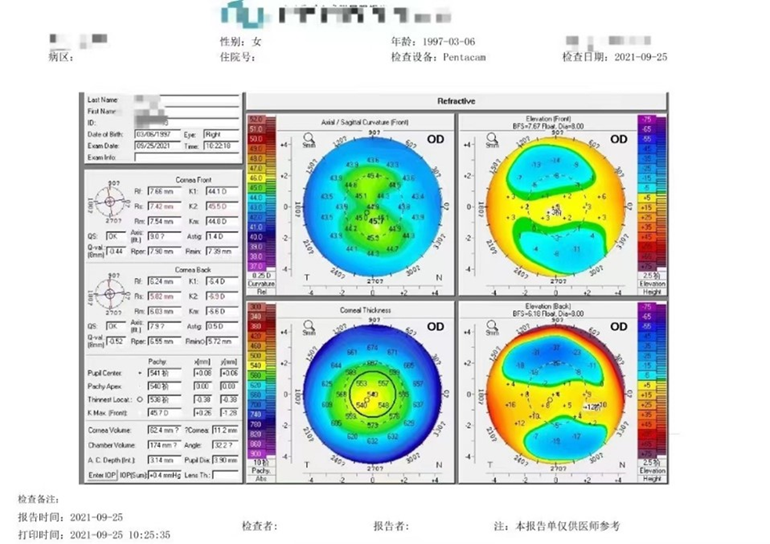
屈光术后B/F ratio=82.2%这一默认值发生了变化，EKR认为是前表面的改变导致了该值的变化，而标准的IOL计算公式是在B/F ratio为82.2%的基础上建立的，由==82.2%推测未手术前R_m前=7.34mm、K_m=1000=46D，该值可以与Holladay Report中的EKR值进行比较(这里未给出图例)，理论上应该相差不大。实际上，该患者B/F ratio=6.03/7.54=80%，K_m=44.8D，屈光力变化为46-44.8=1.2D，由此可以看出，所谓的等效是和标准的B/F ratio为82.2%的模型眼的SimK等效，离B/F ratio为82.2%越近，误差越小。在Petacam中EKR的计算是基于4.5mm内，采用光线追迹技术得到真实的角膜屈光力，可以用于屈光手术后的人工晶体度数计算，一般采用4.5mm区域EKR值带入计算。

角膜并非真正的完美的理想光学面，是中央凸、周边平坦一些的非球面，具有球面像差，且前、后表面具有各自的光学特性，所以以理想光学球面计算出的屈光力都不是角膜的真实屈光力，从而产生了TCRP，采用光路追迹(又称光线跟踪或光路追踪)，同时，还考虑了前后表面、球面像差的存在，即周边和中央屈光力的不同，运用真实的角膜折射率进行计算。可以看出，光路追迹法是一种不依赖于角膜屈光指数的方法，特别是对于角膜屈光术后角膜曲率的测定较其他方法要准确，理论上，TCRP的准确性要更高一些，遗憾的是，虽然准确，但也不能带入基于1.3375的经典度数计算公式。

各个K值采用的方法不一样，描述问题的角度也不一样，具有差异是必然的，它们之间有共性也有个性，有联系也有区别，运用时，需要根据具体情况具体分析，多方比较和不断修正，做出优化选择和配适。最后强调一点，在计算时K值的优选需要参考以视轴为中心的K值，一来，中心区域更能真实的反映角膜曲率；二来，因为斯泰尔斯-克劳福德(Stiles-Crawford)效应的存在，与周边相比，中央区域的光敏感性更高，对视力的影响也更大，故选择中央区域更符合生理。

以上就是对Pentacam地形图中屈光力的一点自己的理解，有不对之处还望批评指正。